ECUACIONES EXPONENCIALES Y LOGARÍTMICAS

FUNCIONES HERMANAS 

La función exponencial es siempre la inversa de la función logarítmica y ésta, a su vez, es siempre la inversa de la función exponencial. Por eso se dice que ambas funciones son "hermanas".

También es importante informar que la palabra logaritmo procede de dos palabras griegas:lógos que significa:razón,relación, manera, estilo  y arithmós que significa número.

Los logaritmos fueron una herramienta muy importante antes de que surgieran las calculadoras científicas y los ordenadores.

Hablemos de F. Exponencial:

Se llama función exponencial a aquella cuya expresión es: f ( x ) = k . ax + b Esta función tiene por dominio de definición el conjunto de los números reales, y cuenta con una característica particular, ya que su derivada es la misma función.

En la expresión f ( x ) = k . ax + b, el número k es real y distinto de cero, mientras que a es un número real positivo y distinto de uno.

Exponencial: a^y= x

Casos en la Aplicación Profesional: 

Sirve para describir cualquier proceso que evolucione de todo aumento o disminución de un pequeño intervalo .

Imaginemos en la  Seguridad Industrial

Su importancia radica en que muchos procesos naturales y sociales están regidos por leyes en cuya expresion  aparece la funcion exponencial esto es ,una variable crece o  disminuye exponencialmente ,con respecto a otra .Se puede aplicar en la desintegracion de un nucleo radioactivo ,cantidad de obreros,que trabajan en una area de la industria o en el calculo de interes simple .

Ejercicios Resueltos:

Ejemplo con  gráfico :

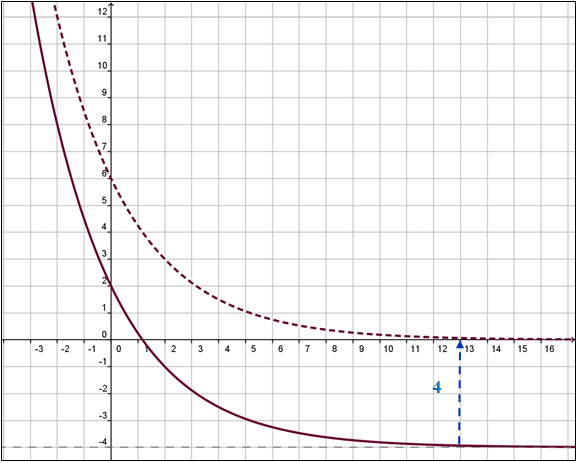
-Determinar si la función representada por la siguiente gráfica es una función exponencial.

Solución:

Paso 1. Mover la gráfica hacia arriba o hacia abajo para que su asínotota horizontal sea y=0. Vemos que en este caso, la gráfica está desplazada hacia abajo. Observamos que a medida que crece el valor de x, la gráfica se acerca a la recta y=-4, por lo tanto esta recta es la asíntota de la función. También notemos que la función es decreciente.	Paso 2. Si la función es decreciente determinar si existe una valor constante  tal que al avanzar las  unidades a la derecha, el valor de y se reduce por la mitad. .Vemos por ejemplo, partiendo de (-2,12) que el valor de y se reduce a la mitad cada 2 unidades de avance en x. Por lo tanto, la gráfica es una transformación de$$f$$ x = 1 2 x 2
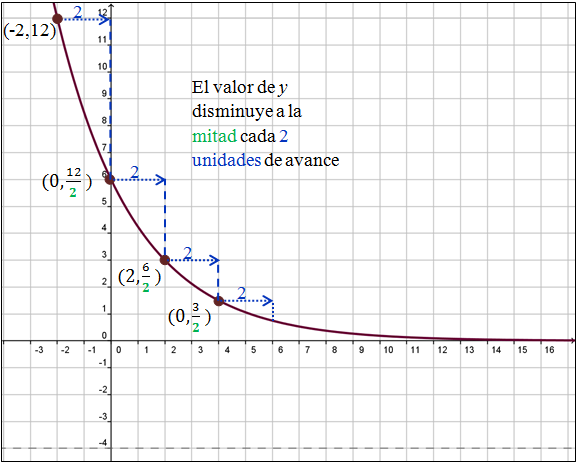En conclusión.- La gráfica si corresponde a una función exponencial.

Función logarítmica:

La función logarítmica es del tipo f ( x ) = logb x donde b representa a un número real distinto de 1 y x es siempre mayor que 0  R; b = 1; x > 0 .
    
Logarítmico: log_ax = y

Es una gráfica que no corta al eje y, a me¬dida que x toma valores cada vez más próximos al 0, y toma valores cada vez menores. La gráfica muestra que la función es creciente, y corta al eje x en 1 porque todo número distinto de 0 elevado a la 0 da por resultado 1. Por lo tanto, en la función logarítmica la asíntota es vertical.

Curiosidades :

•  Cuando en un partido de futbol se produce un saque de meta, el trayecto de la pelota puede ser graficado de acuerdo a la función exponencial. Lo mismo ocurre en los line out del rugby. 

•   Las funciones exponenciales son muy útiles, entre otras cosas, para conocer cuantos habitantes habrá en una región determinada. 
• Los logaritmos se aplican con el claro ejemplo de los estudios de Mendel, quien se dedicó a estudiar el comportamiento de ciertas plantas. En esta categoría es donde se realizan los mayores avances de la humanidad por que cada año descubren miles de fórmulas científicas. 
• Los biólogos lo utilizan para estudiar los efectos nutricionales de los organismos.
• Aplicaciones en la ingeniería, de hecho el comportamiento del universo desde el punto de vista científico es una función logarítmica, también sirven para representar comportamientos de crecimientos de comunidades.
• En las ciencias teorices como en las aplicadas ,por ejemplo para resolver la ecuación exponencial que se deriva de los estudios  de crecimiento poblacional  y de las matemáticas financieras ,aun como una calculadora científica muy buena ,se necesitan las funciones logarítmicas para resolverlas .Requiere del planteamiento de ecuaciones logarítmicas para el calculo de la intensidad de un evento ,tal como es el caso de un sismo otro desastre natural.
• También es empleado en el calculo de pH del agua en los tanques para el consumo humano y los trabajadores de una empresa .

• Un antena Logarítmica periódica es un principio direccional  en donde cada elemento resuena a una frecuencia distinta y en una rango determinado .La unión de todos estos elementos resonantes a diferentes frecuencias  en una disposición logarítmica de antena ,hace que se puede construir un sistema resonante con un gran ancho de banda.

Ejercicios Resuelto :

Si deseo saber cuántos meses deberia dejar depositado un capital, a determinado interés mensual del Banco.Si tengo 1000 $ y los deposito a 3% mensual (0.03). ¿Cuánto tiempo los tendré que dejar depositados para obtener 2000 $?

M = C (1+i)^n

2000 = 1000 (1+0.03)^n

Operando me queda:

2 = 1.03^n

La única forma de despejar al exponente es utilizando logaritmos:

log 2 = n * log 1.03

n = log2 / log 1.03 = 23.45 meses.

Obviamente los meses deben ser enteros, así que tomo 24 meses y el monto obtenido es:

 M = 1000 * 1.03^24= 2032.8

RECORDAR

1. Es muy interesante que los logaritmos ayuden a encontrar la medida de la acidez o alcalinidad de una sustancia ( hallar el pH ); por ejemplo no es suficiente decir en ciertos casos que el jugo de limón es ácido, al saber que su pH es 2.3 nos dice el grado exacto de acidez, se necesita ser específicos.  
2. También con la ayuda de logaritmos se puede determinar la magnitud de la fuerza de un sismo, esa ecuación tiene un inconveniente pues solo determinar el movimiento telurico hasta un cierto grado.
3. Las personas se suprimen a pensar que lo único que te puede servir de las matemáticas son saber la adición de números, la sustracción, la multiplicación y la división de estos mismos ; lo cual es un pensamiento muy mediocre para la época y con los avances tecnológicos de esta época.

TRABAJANDO EN EQUIPO

Entrevista -Ec. Manuel Herrera / MPT

"LAS PROPOSICIONES MATEMÁTICAS,EN CUANTO TIENE QUE VER CON LA REALIDAD,NO SON CIERTAS Y EN CUENTO QUE SON CIERTAS,NO TIENEN NADA QUE VER CON LA REALIDAD."

Albert Einstein  (1879 -1955?) / Científico estadounidense e origen alemán 

Funciones: un concepto fundamental para las matemáticas y su enseñanza .

Michèle Artigue  
Universidad de París, Francia.

Al inicio  del  siglo  veinte, el matemático  Felix Klein, expresando  una  visión  compartida  en  esta  época  por  prominentes  matemáticos, escribió:   “Nosotros,  los  llamados  reformadores,  queremos  colocar  el  centro de la enseñanza en el concepto de función como concepto  de  la  Matemática  de  los  dos  últimos  siglos  que  desempeña  el  papel  fundamental  en  cuantos  sitios  intervienen  nociones  matemáticas.” (Klein, 1924, p.5).

Revista Técnica de la Facultad de Ingeniería Universidad del Zulia

Rev. Téc. Ing. Univ. Zulia 

Programación matemática difusa aplicada en la planeación de requerimientos de material (MRP) 

Un enfoque racional para la toma de decisiones debe tener en cuenta la subjetividad humana, en lugar de emplear sólo medidas con distribución de probabilidad. Esta actitud hacia la incertidumbre del comportamiento humano ha llevado al estudio de un relativamente nuevo campo de análisis de decisión como es, la toma de decisiones difusas, la cual incorpora la subjetividad y la imprecisión en la formulación de modelos y procesos de solución y representa una atractiva herramienta de ayuda a la investigación en ingeniería industrial cuando la dinámica de las decisiones están limitadas por imprecisiones en los modelos formulados. El presente artículo hace un resumen de las aplicaciones que ha tenido la lógica difusa en el campo industrial y presenta un modelo MRP al cual se aplican algunos de estos conceptos. 


La ingeniería industrial ha sufrido importantes cambios con el mejoramiento de las tecnologías de la información, las cuales han permitido dimensionar la planificación de la producción a contextos considerados hasta hace sólo 30 años como inmanejables; así por ejemplo, el análisis sobre la demanda de un producto en particular estaba sujeto en la mayoría de los casos a las conclusiones obtenidas del análisis de una serie de tiempos sin tener en consideración otras variables como son los tiempos de suministro, costos de operación, por lo que los métodos de planificación no eran lo suficientemente apropiados para contar con planes de producción óptimos, esto es la satisfacción de la demanda al costo más bajo. Tanto los nuevos desarrollo en hardware y software, han permitido un redireccionamiento de la planificación, dado que con ellos se ha logrado integrar no sólo variables lógicas si no también ambiguas o difusas. 

GRANDES APORTES DE PROFESIONALES SOBRE F.LINEALES

APORTES DE PROFESIONALES  RECONOCIDOS SOBRE F.LINEALES 

Modelos Deterministas: 

Optimización Lineal

Por:  Dr. Hossein Arsham 
Profesor:Escuela Merrick de Negocios de la Universidad de Baltimore. Escuela de Negocios Merrick/
EE.UU.

Nos comenta sobre un  Modelo de Optimizacion :

"Un modelo de Optimización Matemática consiste en una función objetivo y un conjunto de restricciones en la forma de un sistema de ecuaciones o inecuaciones. Los modelos de optimización son usados en casi todas las áreas de toma de decisiones, como en ingeniería de diseño y selección de carteras financieras de inversión ."

Los problemas de toma de decisiones se pueden clasificar en dos categorías: modelos de decisión determinísticos y modelos de decisión probabilísticos. En los modelos deterministicos, las buenas decisiones se basan en sus buenos resultados. Se consigue lo deseado de manera "determinista", es decir, libre de riesgo. Esto depende de la influencia que puedan tener los factores no controlables, en la determinación de los resultados de una decisión y también en la cantidad de información que el tomador de decisión tiene para controlar dichos factores.

Aquellos que manejan y controlan sistemas de hombres y equipos se enfrentan al problema constante de mejorar (por ejemplo, optimizar) el rendimiento del sistema. El problema puede ser reducir el costo de operación y a la vez mantener un nivel aceptable de servicio, utilidades de las operaciones actuales, proporcionar un mayor nivel de servicio sin aumentar los costos, mantener un funcionamiento rentable cumpliendo a la vez con las reglamentaciones gubernamentales establecidas, o "mejorar" un aspecto de la calidad del producto sin reducir la calidad de otros aspectos. Para identificar la mejora del funcionamiento del sistema, se debe construir una representación sintética o modelo del sistema físico, que puede utilizarse para describir el efecto de una variedad de soluciones propuestas.

Medición de la eficiencia en el sector avícola mediante índices de Malmquist

Lc. Chirinos González, Alira

Licenciada  en Contaduría Pública; M. Sc. en Gerencia de Empresas; Profesora de la Facultad de Ciencias Económicas y Sociales de la Universidad del Zulia-Venezuela.

"El sector avícola es uno de los sectores productivos más importantes de Venezuela y para el cual resulta de vital importancia la medición de la productividad, ya que debe hacer un uso eficiente de sus recursos para así poder mantener unos costos que le permitan fijar los precios cumpliendo con las regulaciones establecidas por el gobierno nacional y obtener el nivel de rentabilidad esperado."

Existe una técnica llamada DEA fue desarrollada inicialmente por Charnes, Cooper y Rodhes en 1978, para calcular el índice de eficiencia técnica resolviendo un programa matemático de optimización, y puede ser considerada como una aplicación al caso de múltiples outputs del análisis tradicional de ratios propuesto por Farrell en 1957. En esta especificación para construir la frontera eficiente se parte de los supuestos de rendimientos constantes a escala, convexidad, así como libre disponibilidad de inputs y de outputs.

Ventajas del análisis envolvente de datos (DEA):

La principal ventaja es que no está basado en el conocimiento de la función de producción, siendo un método no paramétrico, permitiendo así modelos más ricos y no dependientes de los precios de los recursos y productos; además se pueden incorporar las economías de escala. Se puede utilizar en DMU que utiliza múltiples entradas para generar múltiples salidas, donde no se requiere ninguna relación  funcional entre ellas para hallar la función de fronteras; esta se obtiene de información extraída de los datos.

Por otra parte, está la posibilidad de estimar econométricamente la función de producción, lo que ha permitido el desarrollo del concepto de frontera estocástica, que a su vez ha dado el nombre a la segunda metodología en el estudio de la eficiencia, la cual tiene un carácter paramétrico, en cuanto a que se postula una forma funcional especifica para explicar el comportamiento eficiente de las empresas, por lo que los índices de eficiencia obtenidos tienen propiedades estadísticas, permitiendo plantear contrastes de hipótesis a los resultados.

Índice de Malmquist

Otra de las técnicas utilizada para la evaluación de la productividad está basada en los índices de productividad de Malmquist introducidos por Caves, Christensen y Diewert en el año 1982. «El análisis de rendimiento descansa en el concepto de función de distancia, que por su capacidad para  caracterizar la tecnología de producción, se está convirtiendo en la actualidad en la piedra angular del análisis de eficiencia y productividad en las actividades».

Determinación del comportamiento bajo cargas concentradas de perfiles de lámina delgada (MM)

Maritzabel Molina Herrera

Javier Alberto Ortiz Porras

Ingeniera civil, Universidad Nacional de Colombia. M.Sc. en Estructuras, Universidad Nacional de Colombia.
Ingeniero civil, Universidad Industrial de Santander, Colombia. M.Sc. en Estructuras Universidad Nacional de Colombia, Bogotá. 

"En el campo de la lámina delgada continuamente aparecen nuevos tipos de perfiles que son desarrollados con el objeto de mejorar los ya existentes. Un ejemplo de esto es la aparición del perfil M, elaborado para mejorar la eficiencia a corte del perfil C y su resistencia al arrugamiento del alma por efecto de cargas concentradas. Teóricamente, se logra el objetivo de mejorar la resistencia a corte del perfil C y de algún modo su resistencia al arrugamiento del alma, pero debido a los dobleces generados en el alma (rigidizadores intermedios) para acortar la longitud de pandeo, se producen comportamientos que desde el punto de vista de esfuerzos por flexión y deflexiones no pueden ser analizados con los fundamentos teóricos de la mecánica tradicional."

Por la razón expuesta anteriormente, a parte de la determinación de la resistencia teórica del perfil M (basada en el AISI 1996), se desarrollan pruebas sobre cuatro modelos de los que se obtienen tópicos como: carga máxima resistida, identificación visual del posible tipo de falla, deflexiones (centro de la luz) y deformaciones unitarias (εx, εy, εxy), y adicionalmente se elaboran modelos matemáticos simplificados y por elementos finitos (en el programa COSMOS/M), con el fin de hacer una revisión detallada del comportamiento de los esfuerzos y deformaciones en el perfil.

Modelo matemático simplificado

Este método se basa en la determinación de cortantes, momentos y deflexiones, haciendo uso de la estática y de la integración de la ecuación del momento flexionante (Timoshenko, 1986).

Deflexiones.

Modelo matemático utilizando el método de los elementos finitos

La realización del modelo matemático basado en el método de los elementos finitos fue llevada a cabo mediante la utilización del programa COSMOS/M.

Los modelos están constituidos básicamente por elementos laminares (shell).

Además de hacer un análisis numérico de tipo lineal, para los modelos 1 y 2 se realizaron análisis no lineales (no linealidad del material y no linealidad geométrica) con el objeto de estudiar con más detalle el comportamiento de esfuerzos y deformaciones que se presentan en el perfil.

Resultados de los modelos matemáticos por el método de los elementos finitos

INTRODUCCIÓN A LAS FUNCIONES LINEALES

CONOZCAMOS COMO INTERPRETAR UNA FUNCIÓN LINEAL 

1.-Primero es necesario conocer lo términos.

¿QUE ES UNA FUNCIÓN  ?

Una función es una representación algebraica de un fenómeno social o natural; ésta nos permite predecir el comportamiento de dicho fenómeno si alteramos alguna de sus condiciones. 

2.-Ahora acompañado de  LINEAL  :

¿QUE ES UNA FUNCIÓN LINEAL?

Así , la función lineal se convierte en un concepto básico no sólo para las Matemáticas sino para la investigación en general en cualquiera de las gamas o carreras profesionales . A través de la función lineal se pueden analizar fenómenos desde : la relación entre el costo unitario de un producto y la cantidad que se puede comprar con “x” cantidad de dinero; la distancia que recorre la luz en determinado tiempo; el crecimiento de una población de moscas de la fruta, en condiciones óptimas, en un tiempo dado;hasta  los intereses que se pagarán por un préstamo a plazos; etc.

La función lineal es un elemento importante en muchas investigaciones, dado que nos permite mantener una actitud científica frente al fenómeno que estudiamos, y nos posibilita elaborar interpretaciones objetivas del mismo.

PUEDES IMAGINARTE Y RESOLVER EL SIGUIENTE CASO :

Como mencionamos en la introducción, la función lineal es de gran utilidad para interpretar fenómenos tanto sociales como naturales,por ejemplo:

 ¿Sabías que la frecuencia con la que cantan los grillos es una función lineal que depende de la temperatura?. La tabla 1 muestra el número de chirridos por minuto que emite el grillo a una temperatura determinada.

¿Puedes determinar la expresión algebraica que relaciona el número de chirridos por minuto (y), con la temperatura (x)?. Probablemente, en este momento no puedas determinar una respuesta ; pero como contamos con conocimientos base  ,  podemos estar plasmando en este momento una relación    ;a ello llamamos función lineal

Entrevista -Administrador "CLÍNICA SANA"

"Los hábitos se forman por repetición, invierte tiempo en mejorar esos hábitos sanos."

Y estos hábitos se forman día a día gracias a las personas que enriquecen nuestra vida a través de buenas enseñanzas ,por eso este blog fue creado para un fin especifico ,el crear un ambiente de publicación  de contenidos  educativos  que fomente la  escritura como medio de comunicación y de conocimiento .  

Por ello ,como equipo de trabajo queremos  dar un agradecimiento a nuestro Líder Jean Carlos Zapata Rojas en el curso de Matemática II.

La admiración te hace fuerte al saber reconocer las grandes virtudes que te muestra en una bandeja de cartón la vida... 

ANTES DE INICIAR

LA TEMPERATURA :COMO FUNCIÓN 

La temperatura de un enfermo a lo largo del día .Observándola nos daremos cuenta que existe una relación entre la hora del día y la temperatura de dicho enfermo .Con solo un vistazo ,se sabrá la fiebre que ha tenido a cualquier hora del día ,así como los intervalos en los que esta sube o desciende ...

Así existen las llamadas  Funciones Lineales quienes  pueden causar temor, pero tú las usas y resuelves  día a día sin querer , así que todo saldrá bien .

Una de las realidades de la vida es la forma en que gran parte del mundo funciona mediante reglas matemáticas. Los sistemas lineales son una de las herramientas de las matemáticas que tienen múltiples usos en el mundo real. La vida está llena de situaciones en las que la salida de un sistema se duplica si la entrada se duplica y en donde la salida se corta a la mitad si la entrada hace lo mismo. Eso es lo que es un sistema lineal y cualquier sistema lineal puede describirse con una ecuación lineal.