GRANDES APORTES DE PROFESIONALES SOBRE F.LINEALES

APORTES DE PROFESIONALES  RECONOCIDOS SOBRE F.LINEALES 

Modelos Deterministas: 

Optimización Lineal

Por:  Dr. Hossein Arsham 
Profesor:Escuela Merrick de Negocios de la Universidad de Baltimore. Escuela de Negocios Merrick/
EE.UU.

Nos comenta sobre un  Modelo de Optimizacion :

"Un modelo de Optimización Matemática consiste en una función objetivo y un conjunto de restricciones en la forma de un sistema de ecuaciones o inecuaciones. Los modelos de optimización son usados en casi todas las áreas de toma de decisiones, como en ingeniería de diseño y selección de carteras financieras de inversión ."

Los problemas de toma de decisiones se pueden clasificar en dos categorías: modelos de decisión determinísticos y modelos de decisión probabilísticos. En los modelos deterministicos, las buenas decisiones se basan en sus buenos resultados. Se consigue lo deseado de manera "determinista", es decir, libre de riesgo. Esto depende de la influencia que puedan tener los factores no controlables, en la determinación de los resultados de una decisión y también en la cantidad de información que el tomador de decisión tiene para controlar dichos factores.

Aquellos que manejan y controlan sistemas de hombres y equipos se enfrentan al problema constante de mejorar (por ejemplo, optimizar) el rendimiento del sistema. El problema puede ser reducir el costo de operación y a la vez mantener un nivel aceptable de servicio, utilidades de las operaciones actuales, proporcionar un mayor nivel de servicio sin aumentar los costos, mantener un funcionamiento rentable cumpliendo a la vez con las reglamentaciones gubernamentales establecidas, o "mejorar" un aspecto de la calidad del producto sin reducir la calidad de otros aspectos. Para identificar la mejora del funcionamiento del sistema, se debe construir una representación sintética o modelo del sistema físico, que puede utilizarse para describir el efecto de una variedad de soluciones propuestas.

Medición de la eficiencia en el sector avícola mediante índices de Malmquist

Lc. Chirinos González, Alira

Licenciada  en Contaduría Pública; M. Sc. en Gerencia de Empresas; Profesora de la Facultad de Ciencias Económicas y Sociales de la Universidad del Zulia-Venezuela.

"El sector avícola es uno de los sectores productivos más importantes de Venezuela y para el cual resulta de vital importancia la medición de la productividad, ya que debe hacer un uso eficiente de sus recursos para así poder mantener unos costos que le permitan fijar los precios cumpliendo con las regulaciones establecidas por el gobierno nacional y obtener el nivel de rentabilidad esperado."

Existe una técnica llamada DEA fue desarrollada inicialmente por Charnes, Cooper y Rodhes en 1978, para calcular el índice de eficiencia técnica resolviendo un programa matemático de optimización, y puede ser considerada como una aplicación al caso de múltiples outputs del análisis tradicional de ratios propuesto por Farrell en 1957. En esta especificación para construir la frontera eficiente se parte de los supuestos de rendimientos constantes a escala, convexidad, así como libre disponibilidad de inputs y de outputs.

Ventajas del análisis envolvente de datos (DEA):

La principal ventaja es que no está basado en el conocimiento de la función de producción, siendo un método no paramétrico, permitiendo así modelos más ricos y no dependientes de los precios de los recursos y productos; además se pueden incorporar las economías de escala. Se puede utilizar en DMU que utiliza múltiples entradas para generar múltiples salidas, donde no se requiere ninguna relación  funcional entre ellas para hallar la función de fronteras; esta se obtiene de información extraída de los datos.

Por otra parte, está la posibilidad de estimar econométricamente la función de producción, lo que ha permitido el desarrollo del concepto de frontera estocástica, que a su vez ha dado el nombre a la segunda metodología en el estudio de la eficiencia, la cual tiene un carácter paramétrico, en cuanto a que se postula una forma funcional especifica para explicar el comportamiento eficiente de las empresas, por lo que los índices de eficiencia obtenidos tienen propiedades estadísticas, permitiendo plantear contrastes de hipótesis a los resultados.

Índice de Malmquist

Otra de las técnicas utilizada para la evaluación de la productividad está basada en los índices de productividad de Malmquist introducidos por Caves, Christensen y Diewert en el año 1982. «El análisis de rendimiento descansa en el concepto de función de distancia, que por su capacidad para  caracterizar la tecnología de producción, se está convirtiendo en la actualidad en la piedra angular del análisis de eficiencia y productividad en las actividades».

Determinación del comportamiento bajo cargas concentradas de perfiles de lámina delgada (MM)

Maritzabel Molina Herrera

Javier Alberto Ortiz Porras

Ingeniera civil, Universidad Nacional de Colombia. M.Sc. en Estructuras, Universidad Nacional de Colombia.
Ingeniero civil, Universidad Industrial de Santander, Colombia. M.Sc. en Estructuras Universidad Nacional de Colombia, Bogotá. 

"En el campo de la lámina delgada continuamente aparecen nuevos tipos de perfiles que son desarrollados con el objeto de mejorar los ya existentes. Un ejemplo de esto es la aparición del perfil M, elaborado para mejorar la eficiencia a corte del perfil C y su resistencia al arrugamiento del alma por efecto de cargas concentradas. Teóricamente, se logra el objetivo de mejorar la resistencia a corte del perfil C y de algún modo su resistencia al arrugamiento del alma, pero debido a los dobleces generados en el alma (rigidizadores intermedios) para acortar la longitud de pandeo, se producen comportamientos que desde el punto de vista de esfuerzos por flexión y deflexiones no pueden ser analizados con los fundamentos teóricos de la mecánica tradicional."

Por la razón expuesta anteriormente, a parte de la determinación de la resistencia teórica del perfil M (basada en el AISI 1996), se desarrollan pruebas sobre cuatro modelos de los que se obtienen tópicos como: carga máxima resistida, identificación visual del posible tipo de falla, deflexiones (centro de la luz) y deformaciones unitarias (εx, εy, εxy), y adicionalmente se elaboran modelos matemáticos simplificados y por elementos finitos (en el programa COSMOS/M), con el fin de hacer una revisión detallada del comportamiento de los esfuerzos y deformaciones en el perfil.

Modelo matemático simplificado

Este método se basa en la determinación de cortantes, momentos y deflexiones, haciendo uso de la estática y de la integración de la ecuación del momento flexionante (Timoshenko, 1986).

Deflexiones.

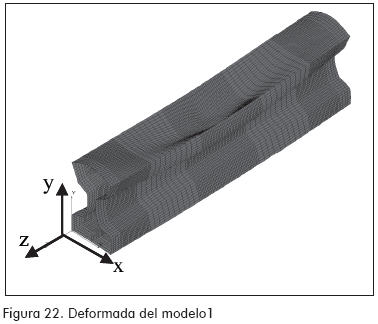
Modelo matemático utilizando el método de los elementos finitos

La realización del modelo matemático basado en el método de los elementos finitos fue llevada a cabo mediante la utilización del programa COSMOS/M.

Los modelos están constituidos básicamente por elementos laminares (shell).

Además de hacer un análisis numérico de tipo lineal, para los modelos 1 y 2 se realizaron análisis no lineales (no linealidad del material y no linealidad geométrica) con el objeto de estudiar con más detalle el comportamiento de esfuerzos y deformaciones que se presentan en el perfil.

Resultados de los modelos matemáticos por el método de los elementos finitos